ARTIGO

 

Um convite a provas sem palavras

 

Claudi Alsina; Roger B. Nelsen

 

 

O que são "provas sem palavras"? Como você verá no presente artigo, a questão não tem uma resposta simples e concisa. Em geral, provas sem palavras são imagens ou diagramas que ajudam o leitor a ver por que razão uma afirmação matemática específica pode ser verdadeira, e também como se pode começar a provar a veracidade dela. Enquanto Yuri Ivanovich Manin disse, "uma boa prova é aquela que nos torna mais sábios", um sentimento ecoado por Andrew Gleason: "as provas realmente não estão lá para te convencer de que algo é verdadeiro - elas estão lá para lhe mostrar por que é verdadeiro".

As provas sem palavras (PWWs, na sigla em inglês) são temas regulares em dois periódicos publicados pela Associação Americana de Matemática. As PWWs começaram a aparecer na Mathematics Magazine por volta de 1975, e no College Mathematics Journal cerca de dez anos mais tarde. Muitas delas aparecem em duas coleções sobre PWWs publicadas pela Associação Americana de Matemática 8, 9.

Mas as PWWs não são inovações recentes - elas estão presentes já há algum tempo, talvez aparecendo primeiro na Grécia antiga e na China e, mais tarde, no décimo século Árabe e na Itália renascentista. Hoje as PWWs aparecem regularmente em periódicos publicados em todo o mundo e na rede mundial de computadores.

Alguns argumentam que as PWWs não são realmente "provas", nem são, aliás, "sem palavras", por conta das equações que frequentemente as acompanham. Martin Gardner, em seus "Jogos matemáticos populares", coluna da edição de outubro de 1973 da revista Scientific American, discutiu as PWWs como diagramas do tipo "olhar – ver". Ele disse: "em muitos casos, uma prova fraca pode ser complementada por um análogo geométrico, de modo tão simples e belo que a verdade de um teorema é quase vista de relance". É nesse espírito que nós escrevemos este "convite" para as PWWs. Em alguns casos, incluímos uma ou duas equações para orientar o leitor, mas a ênfase está claramente em fornecer pistas visuais para estimular o pensamento matemático. Encorajamos o leitor a pensar sobre como a imagem "prova" o teorema antes de ler sobre ele. No entanto, em cada caso, foi incluída uma breve descrição do que esperamos que o leitor veja em cada imagem.

Nós acreditamos que há um papel para as PWWs no ensino da matemática em escolas, do ensino fundamental às universidades. A capacidade de visualizar é essencial para o sucesso em matemática, e a afirmação de George Pólya "desenhe uma figura..." é um conselho pedagógico clássico.

 

Provas combinatórias

As PWWs podem ser empregadas em muitas áreas da matemática, para provar teoremas em geometria, na teoria dos números, trigonometria, cálculo, desigualdades, e assim por diante. No nosso "convite" examinaremos apenas uma área: a combinatória elementar. Em vários teoremas sobre os números naturais {1,2,...} pode-se ter um insight ao representar os nímeros como conjuntos de objetos. Já que a escolha de objeto em particular não é importante, nas PWWs geralmente utilizamos pontos, quadrados, bolas, cubos e outros objetos que podem ser facilmente desenhados.

Neste artigo, vamos utilizar métodos de prova combinatória baseados em dois princípios simples de contagem que podem ser aplicados em representações de números naturais por conjuntos de objetos.

Os princípios são:
1. Se você contar os objetos de um conjunto de duas maneiras diferentes, você obterá o mesmo resultado; e
2. Se dois conjuntos estão em uma correspondência de um para um, então eles têm o mesmo número de elementos.

O primeiro princípio foi chamado de Princúpio Fubini 11 inspirado no teorema de cálculos multivariáveis a respeito da troca n a ordem de integração em integrais iterativos. Chamamos o segundo de Princípio Cantor, em homenagem a Georg Cantor (1845-1918), que o utilizou extensivamente em suas investigações sobre a cardinalidade de conjuntos infinitos. As duas provas técnicas são também conhecidas como o método de dupla contagem e o método de bijeção, respectivamente.

 

Números figurativos

A ideia de representar um número através de um conjunto de objetos (talvez como seixos na praia) remonta, pelo menos, aos gregos antigos. Quando essa representação toma a forma de um polígono tal como um triângulo ou um quadrado, o número é normalmente chamado de um número figurativo. Começaremos com alguns teoremas e provas sobre os números figurativos mais simples: os números triangulares e quadrados.

Quase todas as biografias do grande matemático Carl Friedrich Gauss (1777-1855) relatam a seguinte história. Quando Gauss tinha cerca de 10 anos, seu professor de aritmética perguntou aos alunos da classe para calcular a soma 1 + 2 + 3 +... + 100, prevendo que isso manteria os alunos ocupados por algum tempo. Ele mal terminara a explicação do problema, quando o jovem Carl veio para a frente e colocou sua lousa sobre a mesa do professor com a resposta correta: 5050. Quando lhe pediram para explicar, Gauss admitiu que reconhecera o padrão 1+100 = 101, 2 + 99 = 101, 3+98=101, e assim por diante até 50 + 51=101. Uma vez que existem 50 pares como esses, a soma deve ser 50¡Á101= 5050. O padrão para a soma (adição do maior número com o menor, do segundo maior com o segundo menor, e assim por diante) ¨¦ ilustrado na figura 1, na qual as linhas de bolas representam números inteiros positivos.

 

 

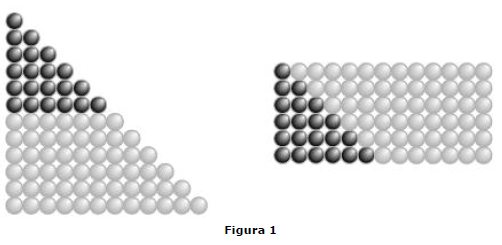
O número tn = 1 + 2 + 3 +... + n como um número inteiro positivo n é chamado de n¡ã número triangular, do padrão de pontos à esquerda na figura 1. O jovem Carl corretamente computou t₁₀₀ = 5050. No entanto, essa solução funciona apenas quando n for ímpar, então primeiro temos que provar

Teorema 1. Para todo n ≥ 1, tn = n (n +1)
                                                   2

Prova. Veja figura 2

 

 

Organizamos duas cópias de t n para formar um arranjo retangular de bolas em n fileiras e n +1 colunas. Então temos 2tn = n(n +1), ou tn = n (n +1)/2.

O procedimento de contagem na prova combinatória anterior é o princípio de Fubini.

Aplicamos o mesmo procedimento para provar que a soma de npumeros ímpares resulta em quadrados.

Teorema 2. Para todo n ≥ 1, 1+3+5+...+(2n - 1) = n².

Prova. Apresentamos duas provas combinatórias na figura 3.

 

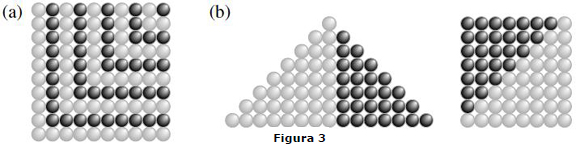
1+2 = 3,
4+5+6 = 7+8,
9+10+11+12 = 13+14+15, etc.

 

Note que cada fileira começa com um número quadrado. O padrão geral

n² +(n² +1)+...+(n² + n) = (n² + n +1)+... +(n² +2n)

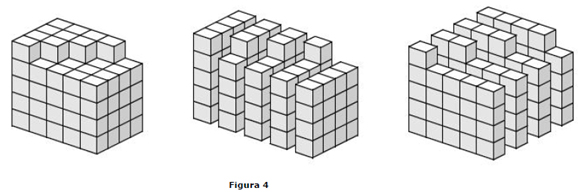
pode ser provado por indução, mas a seguinte prova visual é muito melhor.

Na figura 4, vemos a versão da identidade n = 4 na qual a contagem do número dos cubos pequenos na pilha de dois modos distintos produz 16+17+18+19+20 = 21+22+23+24.

 

Existem muitas relações boas entre números triangulares e quadrados. O mais simples é, talvez, o ilustrado do lado direito da figura 3b: tn-1 + tn = n². Dois outros são dados no seguinte lema (considerando t0 = 0 por conveniência):

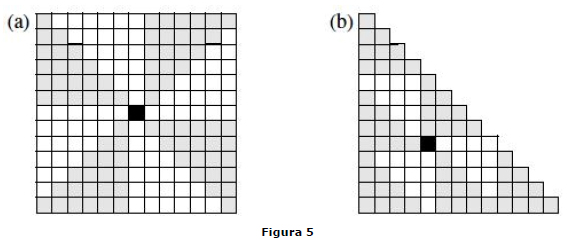
Lema 1. Para todo n ≥ 0, (a) 8tn = 1 = (2 n +1)², e (b) 9tn +1 = t3n +1.

Prova. Veja a figura 5 (na qual substituímos as bolas por quadrados).

 

 

O lema 1 nos permite provar os dois seguintes teoremas.

Teorema 3. Existem infinitamente mais números que são simultaneamente quadrados e triangulares.

Prova. Observe que

 

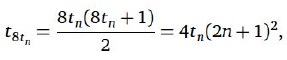
então se tn é quadrado, então o mesmo ocorre com t8tn. Se t1 = 1, essa relação gera uma sequência infinita de números quadrados triangulares, por exemplo, t8 = 6² e t288 = 204².

No entanto, existem números quadrados triangulares como t49 = 35² e t1681 = 1189² que não estão nessa sequência.

Teorema 4. A soma das potências de 9 são números triangulares, isto é, para todo n ≥ 0,

1+9+9² +...+9ⁿ = t1+3+3²+...+3ⁿ

Prova. Veja a figura 6.

 

 

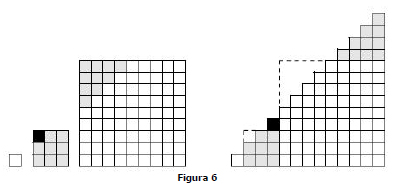
Como consequência, na base 9 os números 1,11,111,1111,... são todos triangulares.

O próximo teorema apresenta um complemento à identidade tn − 1 + t n = n².

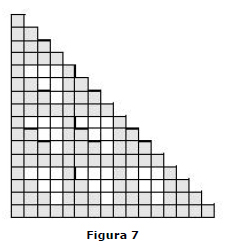
Teorema 5.  A soma dos quadrados dos números triangulares consecutivos é um número triangular, isto ¨¦, 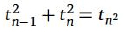 para todo n ≥ 1.

Prova. Veja a figura 7, na qual ilustramos o quadrado de um número triangular como um arranjo triangular de números triangulares.

 

Você deve ter notado que o n¡ã número triangular é um coeficiente binomial, isto ¨¦, t_n = 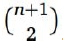. Uma explicação para isso é que cada um é igual a n (n +1)/2, mas esta resposta lança pouca luz sobre o porquê é verdadeiro. Aqui temos uma explicação melhor usando o Princípio de Cantor:

Teorema 6. Existe uma correspondência um a um entre um conjunto de objetos tn e um conjunto de subconjuntos de dois elementos de um conjunto com objetos n+1.

Prova. Veja a figura 8 6, e relembrando que o coeficiente binomial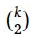

 

 

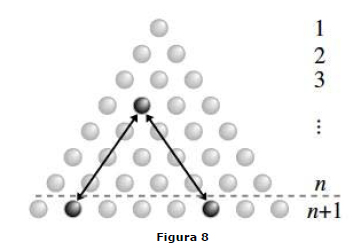
É o número de maneiras para escolher 2 elementos de um conjunto de elementos k. Os arranjos denotam uma correspondência entre um elemento do conjunto com elementos tn e um par de elementos de um conjunto de elementos n+1.

 

4. Soma de números quadrados, triangulares e cubos

Tendo examinado os números triangulares e quadrados como somas de números inteiros e somas de inteiros ímpares, agora consideramos somas de números triangulares e somas de quadrados.

Teorema 7. Para todo n ≥ 1, 1² +2² +3² +... + n² = n (n +1)(2n +1) / 6. Prova. Apresentamos duas provas. A primeira está na figura 9.

 

 

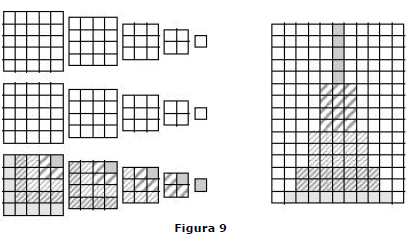
Exibimos a correspondência um a um entre três cópias de 1² + 2² + 3² +... + n² e um retângulo cujas dimensões são 2n + 1 e 1+2+... + n = n(n + 1)/2 4. Uma vez que 3(1² +2² +3² +...+ n²) = (2n+1)(1+2+...+n), segue agora o resultado.

Para uma segunda prova, veja a figura 105.

 

 

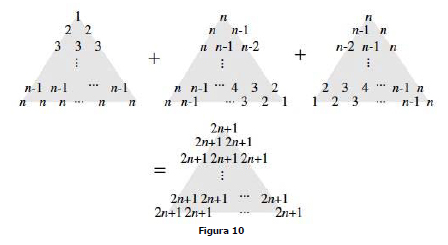
Aqui escrevemos cada quadrado k² como a soma de k ks, então colocamos esses números em um arranjo triangular, criamos mais dois arranjos através da rotação do arranjo triangular em 120¡ã e 240¡ã, e adicionamos componentes correspondentes em cada arranjo triangular.

Teorema 8. Para todo n ≥ 1, t1 + t2 + t3 +...+ tn = n(n +1)(n +2)/6.

Prova. Veja a figura 11.

 

 

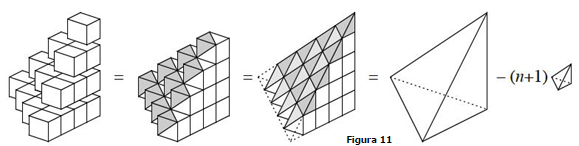
Aqui empilhamos camadas de unidades de cubos para representar os números triangulares. A soma do s números triangulares é o número total de cubos, que é o mesmo que o volume total dos cubos. Para calcular o volume, "fatiamos" pirâmides pequenas (sombreadas) e colocamos cada pequena pirâmide no topo do cubo de onde ela veio. O resultado é uma grande pirâmide triangular direita menos algumas pirâmides triangulares menores ao longo de uma extremidade da base. Assim

 

 

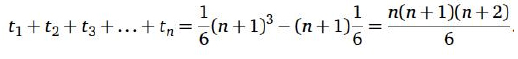
Na prova acima avaliamos a soma dos primeiros números triangulares n através do cálculo dos volumes das pirâmides. Isto é, na verdade, uma extensão do Princípio de Fubini pela simples enumeração de objetos para medidas aditivas tais como o comprimento, área e volume. A versão do volume no Princípio de Fubini é: calcular o volume de um objeto de duas maneiras diferentes produz o mesmo número, e o mesmo ocorre de forma semelhante para o comprimento e a área. Não se pode, no entanto, estender o Princípio de Cantor para medidas aditivas - por exemplo, pode-se construir uma correspondência de um -para-um entre os pontos sobre dois segmentos de reta com diferentes comprimentos.

Teorema 9. Para todo n ≥ 1, 1³ +2³ +3³ +... + n³ = (1+2+3+...+ n)³ =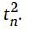

Prova. Novamente, podemos dar duas provas. Na primeira, representamos k³ como k cópias de um quadrado com área k³ para estabelecer a identidade 3, 7.

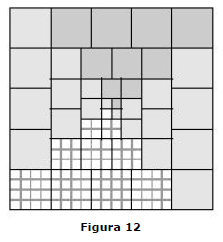
Na figura 12, temos 4(1³ +2³ +3³ +... + n³) = n (n +1)² (para n = 4).

 

 

Como segunda prova usamos o fato que 1+2+3+...+(n − 1)+ n +(n − 1)+...+2+1 = n²

(deixamos como exercício para o leitor desenhar uma figura com bolas em um arranjo quadrado e contar as bolas em diagonais nesse arranjo quadrado) e considerar um arranjo quadrado de números (ao invés de bolas) no qual o elemento na fileira i e na coluna j é i j, e some os números de duas formas diferentes. Veja a figura 13 10.

 

 

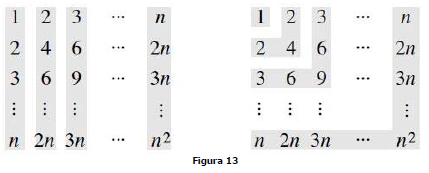
Somando os resultados por colunas

 

enquanto soma dos resultados das regiões sombreadas em forma de L 1 ¡¤ 1² +2 ¡¤ 2² +... + n ¡¤ n² + =

Concluímos esta seção com um teorema representando um cubo como a soma em dobro de números inteiros.

Teorema 10. Para todo n ≥ 1,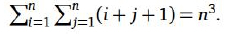

Prova. Representamos a soma em dobro como uma coleção de cubos unitários e calculamos o volume de uma caixa retangular composta por duas cópias da coleção. Veja a figura 14.

 

 

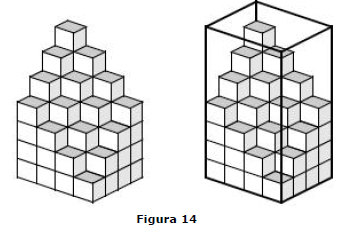
Observe que duas cópias da soma 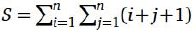cabem dentro da caixa retangular de base n² e altura 2n, consequentemente o cálculo do volume da caixa de duas formas produz 2S = 2n³, ou S = n³.

Conclusão

Nesta curta avaliação vimos provas visuais usando representações de números por
conjuntos de objetos. Naturalmente, há muitas outras maneiras de representar números (não necessariamente números naturais), incluindo sua representação como comprimentos de segmentos, áreas de figuras planas, volumes de objetos. Com tais representações, outras técnicas podem ser utilizadas nas provas, tais como rotações, translações, reflexões e outras transformações que preservem comprimento, área ou volume. Para um exame detalhado dessas técnicas (e muitas outras), veja os livros Math made visual: creating images for understanding mathematics e When less is more: visualizing basic inequalities 1, 2.  

 

Referências bibliográficas

1. C. Alsina and R. Nelsen. Math made visual: creating images for understanding mathematics. Mathematical Association of America, Washington, 2006.

2. C. Alsina and R. Nelsen. When less is more: visualizing basic inequalities. Mathematical Association of America, Washington, 2009.

3. A. Cupillari. "Proof without words". Mathematics Magazine, (62):259, 1989.

4. M. Gardner. "Mathematical games". Scientific American, p.115, October 1973.

5. S. Kung. "Sum of squares". College Mathematics Journal, (20):205, 1989.

6. L. Larson. "A discrete look at 1+2+...+ n". College Mathematics Journal, (16):369382, 1985.

7. W. Lushbaugh. (sem t¨ªtulo). Mathematical Gazette, (49):200, 1965.

8. R. Nelsen. Proofs without words: exercises in visual thinking. Mathematical Association of America, Washington, 1993.

9. R. Nelsen. Proofs without words II: more exercises in visual thinking. Mathematical Association of America, Washington, 2000.

10. F. Pouryoussefi. "Proof without words". Mathematics Magazine, (62):323, 1989.

11. S. Stein. "Existence out of chaos". In: R. Honsberger (editor), Mathematical Plums, pp.6293. Mathematical Association of America, Washington, 1979.

 

 

Tradução: Germana Barata
10/11/2012
Claudi Alsina é professor da Universidade Politécnica da Catalunya, Secci¨® de Matemátiques i Informática, Barcelona, Espanha. Email: Claudio.alsina@upc.edu  
Roger B. Nelsen é professor do Lewis & Clark College, do Departmento de Ciências Matemáticas em Portland Oregon, EUA. Email: nelsen@clark.edu
* Este artigo é uma tradução do original em inglês publicado no periódico European Journal of Pure and Applied Mathematics, Vol.3, no.1, pp.118-127. 2010.